If you don’t know what is maximum flow or minimum cut I suggest you start by reading this tutorial TopCoder Tutorials: Maximum Flow or sections 26.1, 26.2 in Introduction to Algorithms 3rd ed, make sure you understand the equivalence between maximum flow and the size of minimum cut, this tutorial contains some applications and example problems.
Before going through this tutorial let me warn you the problems described here are interesting. you should give yourself some time to think/solve before reading the solution.
Maximum number of disjoint paths in a graph
This is a pretty standard application of maximum flow, given a directed graph find the maximum number of edge disjoint paths between vertices S and T. Two paths are said to be edge disjoint if they no edges in common. From the given graph we construct a flow network where each edge has a capacity of 1, the maximum number of edge disjoint paths is the maximum flow going from S to T, one way to convince your self is that every unit of flow represents a path from S to T, and every edge we have in the graph was used at most once (capacity = 1) thus those paths which we’ve sent the flow across are edge disjoint.
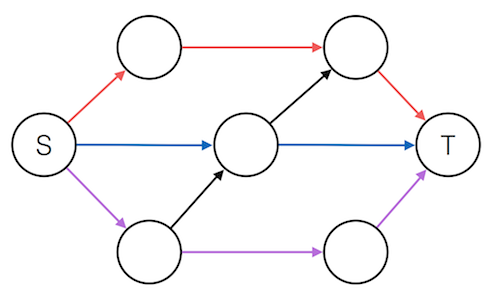
If the problem required maximum number of vertex disjoint paths where each vertex can be used in at most one path except S, T.
To solve this we introduce vertex capacities, where each vertex has a capacity of 1 (except S, T) and each edge has a capacity of ∞.
To enforce vertex capacities we do the following For a vertex x with capacity k we split this vertex into two vertices x_in and x_out where all edges going into the vertex are directed to go into x_in and all edges going out of the vertex are directed to go out of x_out, then we connect x_in and x_out with an edge of capacity k.
Crazy Wall[Andrew Stankevich Contest 17]
Given some bricks where each brick has a start, end we want to build a wall with maximum number of rows where each row in the wall satisfies the following:
- Each row is a sequence of bricks such that each brick starts where the previous brick has ended, first brick starts at 0 and last brick ends at w.
- No two rows have a spacing at the same place, i.e if one row has a brick that ends at position x, no other row should have a brick ending at x, except for bricks that end at w.
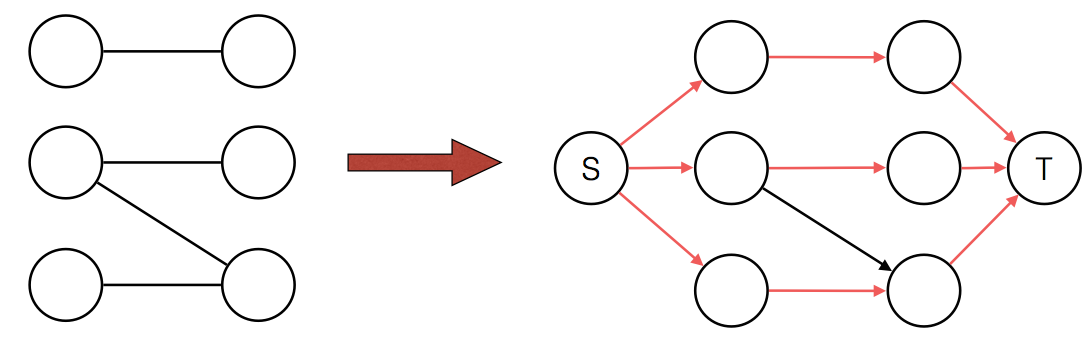
So we want to use the available bricks to build a wall with maximum height, we can model the problem as a graph, where the vertices are places where bricks start, end, and we have an edge between vertex i and vertex j if we have a brick that starts at i and ends at j, now the maximum number of rows we can build is the maximum number of vertex disjoint paths between vertex 0 and vertex w.
Maximum Bipartite matching
A matching in a graph is a subset of the graph edges such that each vertex is incident to at most one edge in this subset, a maximum matching is such a subset with maximum size.
To find the maximum matching in a bipartite graph we construct a flow network containing the original vertices of the graph and all edges with capacity 1, directed from the first set to the second set, we also add two special vertices S, T and connect S to each vertex in the first set with a directed edge with capacity 1, and connect each vertex in the second set to T with a directed edge of capacity 1, the maximum matching then is the maximum flow from S to T.
Cycle cover
Given a directed graph with n vertices find if we can select a some simple cycles in this graph such that each vertex belongs to exactly one cycle.
Well that graph isn’t bipartite!, first observe that in a graph composed of disjoint simple cycles each node has exactly one edge entering and exactly one edge leaving it, also any graph satisfying this condition is composed of disjoint simple cycles, so if we could select some edges from our graph and enforce that condition then we’re done.
We split each vertex V_i into two vertices V_i_out, V_i_in, now if two vertices V_i, V_j were connected by an edge we connect V_i_out to V_j_in, now if this bipartite graph contains a perfect matching(a matching of size n) we can use the edges in this matching to construct the cycles graph, because having a perfect matching means that for each node we’ve selected exactly one outgoing edge, and exactly one incoming edge satisfying the previous condition.
The Swapping Game[ICPC Regionals Arab 2012]
Since we only care about the last state of the string, it’s possible to visit invalid state, we can view this problem as a matching problem where we want to match each position with a character such that the matching is perfect, and the resulting string is lexicographically minimum. We already know how to find a perfect matching (find the maximum matching and see if it’s perfect), however how do we find the lexicographically minimum perfect matching where earlier positions are matched with smaller characters.
It turns out that if we know how to check if there’s a perfect matching or not we can easily find the lexicographically minimum perfect matching, we first take the first position and match it with the smallest character it can be matched with, then check if there’s a perfect matching for the rest of the graph, if so we remove the first position/smallest character from the graph and move on to next position, otherwise we try to match it with the second smallest character, and so on.
Since there’s at most 5 characters to try at each node we end up running the perfect matching check algorithm at most 5n times.
Exercise: Find an O(nm) algorithm that solves the lexicographically minimum perfect matching problem. hint1: start by any matching and try to optimize it. hint2: learn about alternating path algorithm for maximum matching see this and this.
Minimum vertex cover in bipartite graph
A vertex cover in a graph is a subset of vertices such that each edge in the graph is adjacent to at least one vertex in this set, so given a bipartite graph we want to find a vertex cover with minimum number of vertices, in other words we want to find minimum number of vertices that cover the edges of the graph.
One thing to observe is if we remove all vertices in some vertex cover the graph will contain no edges.
Lets construct a flow network using the bipartite graph, S connected to each node in the first set with an edge with capacity 1, each node in the second set is connected to T with an edge with capacity 1, all other edges go from first set to second set with capacity ∞.
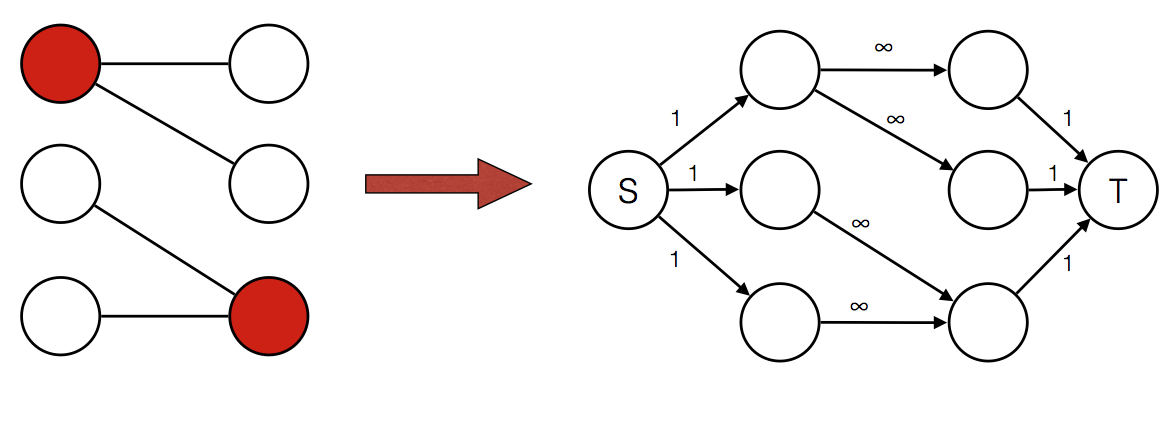Verticies coloured in red are the minimum vertex cover, white ones are the maximum independent set
Now the size of the minimum vertex cover is the maximum flow from S to T, or the maximum matching in the original graph.
But why is that ? First note that a set of vertices X is a vertex cover if and only if after we remove X from the network S will not be connected to T since all edges between first and second set be removed from the graph.
Second observe that removing a node from the network is equivalent to removing the edge that connects that node to S or to T since after we remove that edge this node will never help connecting S to T because other edges at this node will be useless.
Now the problem boils down to finding the minimum weight edges to cut in order to disconnect S from T, obviously those edges will include only edges with capacities (or weights) 1, which is the minimum S-T cut, that’s equivalent to finding the maximum flow from S to T.
A good thing also that the previous method works also if the vertices have weights and we wanted to find the minimum weighted vertex cover, if a vertex P from the first set have weight W, then the edge between S and P should have capacity W, and for a vertex Q from the second set having weight K, then the edge between Q and T should have capacity K.
You might want to check König’s theorem which states that
In any bipartite graph, the number of edges in a maximum matching equals the number of vertices in a minimum vertex cover.
Dungeon of Death
Given an nxn grid, some cells are marked, an operation is defined by covering a full row, or a full column find the minimum number of operations to cover all marked cells.
It’s a covering problem, and we know already that we can use vertices of a bipartite graph to cover edges so we should model marked cells (what we want to cover) as edges, and rows and columns (what we use to cover) as vertices.
We construct a bipartite graph with rows and columns as our vertices, row_i is connected to column_j with an edge if cell i, j is marked, now we the answer is the minimum vertex cover in this bipartite graph.
Cat vs. Dog
Lets construct a bipartite graph where the two sets are cat lovers and dog lovers, add an edge between two vertices if their corresponding persons voted against each other’s will for example if one person voted D1 C2, the other voted C2 D3 then we connect their corresponding vertices with an edge, now we need to remove minimum number of vertices from this graph until we have no person vote against another’s will, that’s equivalent to removing a minimum vertex cover from the graph, the remaining vertices form a Maximum Independent set.
Paratroopers
First notice that we could get rid of multiplication and change it into addition by taking logarithm of all weights i.e log(a*b) = log(a)+log(b), now the problem becomes a direct application of minimum weighted vertex cover in a bipartite graph.
Minimum path cover on a directed acyclic graph
Given a Directed Acyclic graph with n vertices find the least number of paths such that each node belongs to exactly one path.
Assume initially that we had n paths, one path for each node, now if we had some path ending at vertex i, and some other path starting at vertex j, and i is adjacent to j we can then join the two paths together into a single path reducing the number of paths by 1 path.
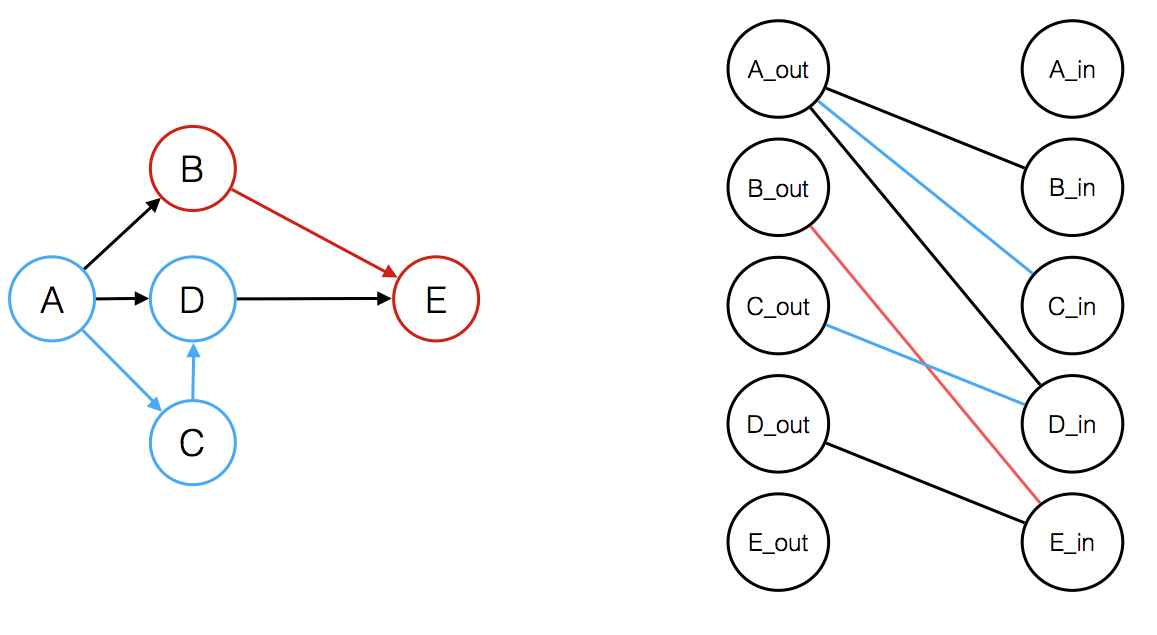
Thus the minimum path cover is achieved when we do maximum number of joins. To obtain the maximum number of joins we construct a bipartite graph by splitting each vertex V_i to V_i_in, and V_i_out, we connect V_i_out to V_j_in if there’s an edge between i and j, the maximum number of joins then is the maximum matching in this bipartite graph.
If we were allowed to visit vertices more than once i.e repeat cover allowed, we then do the same but on the transitive closure of the DAG.
Stock Charts[Google Code jam 2009 - Round 2]
Create a DAG from the given charts, where each vertex corresponds to a chart, vertex V_i has an edge going to V_j if each kth point in the ith chart is less than the kth point in the jth chart, the answer then is the minimum path cover in that DAG.
Animal run
Given a weighted graph on the form of a grid (n by m, n≤1000, m≤1000), where each node is adjacent to it’s four neighbours plus it’s north west neighbour, and it’s south east neighbour, find the minimum cut between the upper left node and lower right node.
That looks like a standard mincut problem, however the number of nodes is very large thus we can’t use max flow to solve it. So our algorithm should make use of the special form of the graph.
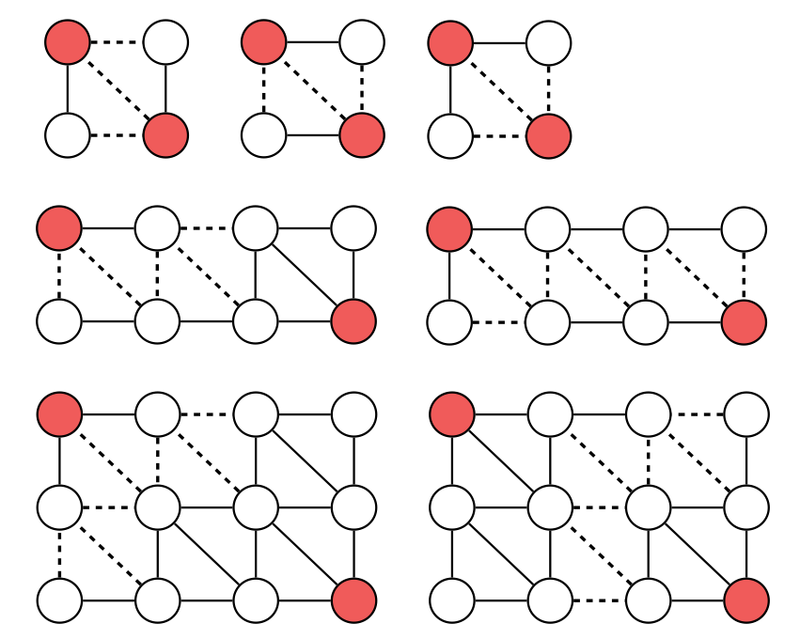After looking at some possible cuts we observe that each triangle contains either zero or two edges cut, because if we cut a single edge in a triangle all three vertices are still reachable from each other, thus cutting this edge is useless.
We also observe that each cut is a path must start at the west or south and go to north or east,cutting two edges per triangle in it’s way.
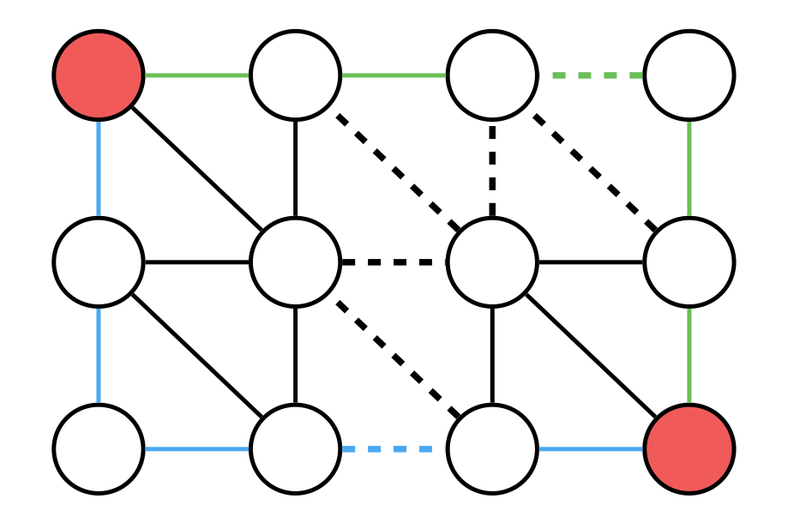
Note that this graph is a Planar graph, and those triangles are called Faces of the graph, and by treating faces as nodes while doing shortest path we are doing shortest path on the Dual graph.
Coconuts
We have two groups of people, first group believes african birds can carry coconuts, the second group believes that they can’t, and we have friendships relations between those people, we are going to ask everyone to vote about what they believe in, they might vote against their beliefs in order to reduce the disagreement with their friends. So they would answer in the manner such that they minimize the number of votes they do against their beliefs plus the number of disagreements between friends, we are to find this minimum number of votes against belief and disagreements.
Lets assume someone believes birds can carry coconuts, and he has three friends who believe birds can’t and won’t vote against their beliefs, then it’s better to vote against his beliefs in order to minimise the result.
We can think about the situation that each person is being attracted to his beliefs and also attracted by his friends who are also attracted by their beliefs, and since a person can only make one vote some bonds has to be cut, in particular mincut!
Lets create a graph where each person corresponds to a node friends are connected to each other, we also have two special nodes S connected by each person who believes that birds can carry coconuts, T connected by each person who doesn’t.
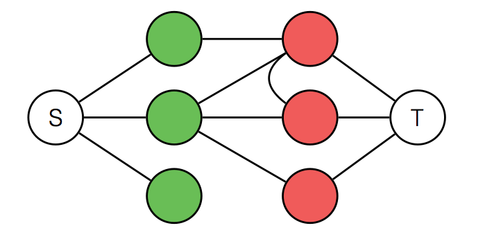
Now imagine if those edges were strings, and we kept moving S and T apart from each other.
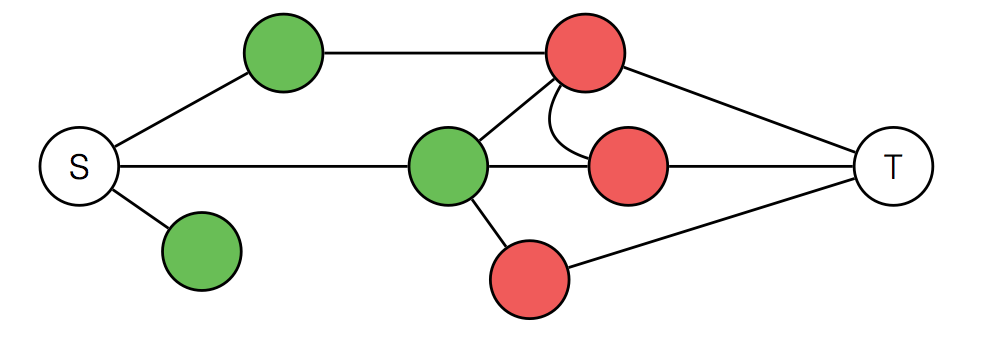
Weak bonds are cut!
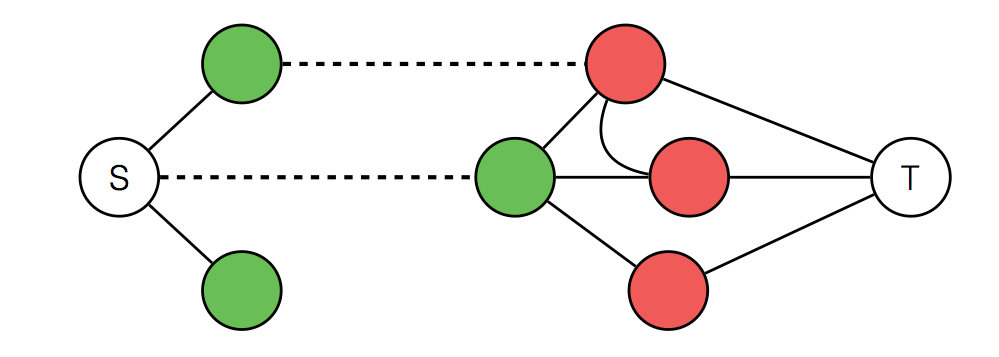
This means that one person votes against his beliefs, and one person disagrees with his friend, so total is 2.
The answer for our problem is the minimum S-T cut!, the general version of this problem is to partition some items into two sets, where each item being not in a specific set has a cost, and each item being in a different set from another item has a specific cost we want to partition the items to minimise the cost, this is also minimum cut with the edges having weight (or capacity if you are going to solve using maximum flow).