Many problems are easier when solved backwards, or maybe impossible to solve if attacked in the straight forward way.
Solving a problem backwards may involve attacking the problem from a different point, thinking about the last step first or starting with the result and try to reach the initial state.
9 Puzzle
We can model the game as a directed graph, where each node is a state of the game, an upper bound on the number of reachable states in each query is indeed 9!, however 9! for each test case is not really nice.
A good thing to note is that the destination state is always the same for every test case, the only different thing is the start state.
What if we reverse the edges of the graph and start from the destination state, and do a single breadth first search from the destination state, caching the distance between the destination state (123456789) and every other state.
Now after (doing) this pre-calculation we can answer each query in O(1).
CasketOfStar [Topcoder SRM 533]
Trying to attack this problem in the usual manner will lead us no where but the (N-2)! where N is the number of stars.
Now lets try to think in reverse, think of the very last step where after this step the stars became just 2.
Lets assume in the beginning we had those stars
A B C D E F G
Now if we know that D was the last star removed, we know that the it’s contribution to the result was A*G, this also tells us that nothing from A, B, C contributed to the result while removing stars E, F because D was there in the middle, and nothing from E, F, G contributed to the result while removing B, C this means that if we removed D last we can split the problem into two subproblems, as we get energy equals A*G + Solution of([A B C D]) + Solution of([D E F G])
Lets take a look of this sequence of removals, C, F, E, B, D in reverse order.
A G, Final state
A D G, Adds A * G
A B D G, Adds A * D
A B D E G, Adds D * G
A B D E F G, Adds E * G
A B C D E F G, Adds B * D
A B C D E F G, Initial state
So how to solve the problem ? from all the stars choose the star that gives maximum result when removed last, solve subproblems recursively of course.
Here’s a recurrence that describes the solution, l and r describe the start and end of the current interval we’re solving the problem for.
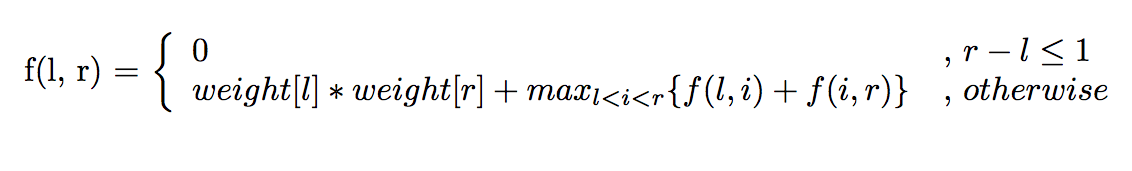
so for each l, r we pick we want the star that which if removed last would maximize the answer.
Counting Arborescence in a DAG
According to wikipedia, an arborescence is a directed graph in which, for a vertex u called the root and any other vertex v, there is exactly one directed path from u to v.
How to count the number of arborescence in a given Directed acyclic graph, of course all arborescence in a DAG must start at the same node, otherwise it won’t be a DAG.
Lets think in reverse again, and assume we do have an almost complete arborescence and we’re adding the very last node to it, that node of course must have no outgoing edges, in other words the last node of some topological sort of that DAG.
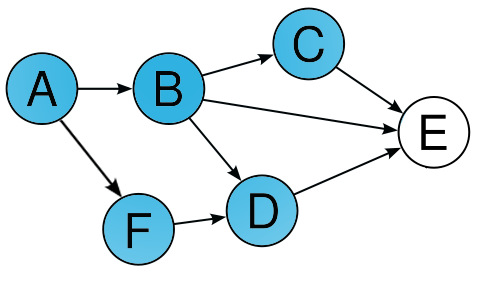
We’re trying to find an arborescence rooted at A, lets assume we’ve solved the problem for nodes A, B, C, D and F, how many ways can we connect A to E ? 3, connect E to any of the nodes connected to A so the number of ways is the number of edges incident to E.
Now the number of arborescence rooted at A, can be calculated as 3 * Number of arborescence for the graph minus E. For the given graph, the number of arborescence would be 3 * 2 * 1 * 1 * 1
To calculate the result for any DAG we can just multiply the in degrees of each of the nodes except the root.
Note that for this to work the root must exist, i.e the graph must have only a single node with zero in degree.
####TreesCount[Topcoder SRM 474]
This problem isn’t really much harder than the previous one, lets first discard all edges that will always be removed, these are the edges that are NOT on any shortest path from node 0 to any other node, and keep only the edges that lie on some shortest path from node 0 to some other node.
These edges can be found easily by using the distance array which contains the shortest path length from node 0 to any other node.
An edge (i->j) that lies on some shortest path from node 0 to some other node will satisfy the following equation
distance[i] = distance[j] + weight[i][j]
These edges alone form a DAG, Why? because the shortest path is always acyclic in a graph where all edge weights are positive.
So now the problem reduces to counting arborescence in that shortest path DAG which we know how to solve.
####Additional problems * Anansi’s Cobweb