Problem divisibility

Divisibility[ICPC Regionals Dhaka 2012]

Before solving the problem lets rephrase it, Given a hypercube in an infinite N dimensional grid where each cell contains the number of paths to the origin, such that each step of each path always decreases the distance between the cell and the origin, find the number of cells in the given cube which contains a number not divisible by a prime P.

First we should begin by thinking how do we calculate the value at each cell, we can think of a simple recurrence like

$F(X_{1},..., X_{N})=\sum_{X_{i}>0} F(X_{1},...,X_{i}-1,...,X_{N})$

But can we find a more direct formula ?

Lets take a look at a simpler problem where the grid is only 2D, the moves allowed are only Left L, or Down D then $F(X_{1}, X_{2})$ is the number of words with length $X_{1}+X_{2}$ , containing exactly $X_{1}$ L’s and $X_{2}$ D’s, this can be calculated easily by choosing location for L’s rest are D’s so the formula becomes

$F(X_{1}, X_{2}) = \binom{X_{1}+X_{2}}{X_{1}}$

For the N dimensional grid we can use the formula multiple times i.e choose locations for the first dimension, then from the rest choose locations for the second dimension and so on.

Another way to solve the problem is to generate all possible words then remove the repetitions

$F(X_{1}, X_{2},...,X_{N}) = \frac{(X_{1} + X_{2} + ... + X_{N})!}{X_{1}! * X_{2}! * ... * X_{N}!}$

Now we got the formula we need to figure out how to check the divisibility by P

The formula above is divisible by P if the power of P in the numerator is strictly greater than the power of P in the denominator.

But how do we calculate the power of P in K! ? In the first K positive numbers we have $\lfloor K/P \rfloor$ numbers divisible by P, $\lfloor K/P^2 \rfloor$ numbers divisible by P^2 we should add those twice (since they add 2 to the power of P) but they are already added once in those numbers divisible by P so we add them once, Numbers divisible by P^3 are also divisible by P^2, and P so we add them once when doing numbers divisible by P, once when doing numbers divisible by P^2 and once when doing numbers divisible by P^3, and so on.

We can write a simple function to calculate this value

int g(int K, int P) {
    int result = 0;
    while(K>0){
        K = K/P;
        result = result + K;
    }
    return result;
}

Repeated division by P hints that looking at K in base P might lead us to something interesting. lets write K in base P as $k_{b}k_{b-1}...k_{0}$ We observe that digit at position b contributes to the prime power b times and each time the contribution decreases by a factor of P using geometric sequence sum we can rewrite the formula as $g(K, P) = \sum_{0 \leq i \leq b} k_{i} * \frac{P^{i} - 1}{P-1}$

Now when is $F(X_{1}, X_{2},...,X_{N})$ divisible by P? The power of P of the denominator is the sum of the power of P in each $X_{i}!$ The power of P in the nominator is the power of P in the factorial of their sum, if we consider adding those N numbers together in base P if carry occurred at the ith digit means that we had sum of ith digits in all the N numbers ≥ P, but how does this change change the power of P ? The ith digit sum has X ≥ P so we have to move at least P from those X to i+1th digit, this would increase the power of P by 1 since $\frac{P^{i}-1}{P-1} = P * \frac{P^{i-1}-1}{P-1}+1$

If carry did not occur we would have the power of P in nominator same as in the denominator.

Thus P divides F if and only if carry occurs while adding all X’s in base P.

Now we can solve the problem the problem for a hypercube start at the origin by using digit dynamic programming, we need to assign values for each digit in each X such that the sum of values in each digit is strictly less than P, and the resulting point is strictly inside the hypercube.

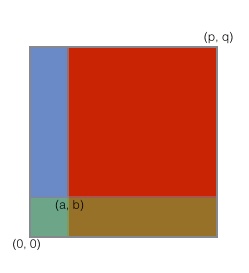
Finally to compute the result for general hypercubes that don’t start at the origin we use Inclusion–exclusion principle for example: if we were to calculate the result for the rectangle starting at (a, b) and ending at (p, q) the result would be F(p, q) - F(a, b-1) - F(a-1, b) + F(a-1, b-1) We add F(a-1, b-1) because it’s subtracted twice

2d-example

if we were to calculate the result for the cube starting at (a, b, c), ending at (p, q, r) this would be F(p, q, r) - F(p, q, r-1) - F(p, q-1, r) - F(p-1, q, r) + F(p, q-1, r-1) + F(p-1, q, r-1) + F(p-1, q-1, r) - F(p-1, q-1, r-1) We are computing the result for cube starting at the origin and ending at (p, q, r) and then we compute the part to remove by using other cubes whose union cover this part.

This problem combines more than one topic, here are some resources/problems for each of them

Number theory

Digit dp

LeftRightGame2

Inclusion Exclusion principle