Ever met a geometry problem that doesn’t have much to do with geometry ? this is the problem we want to discuss today, Mirror trap from the 15th Polish Olympiad in Informatics.
The problem gives you a Simple rectilinear polygon whose all sides are covered from the inside with mirrors, asks you to put some laser guns in some corners, some laser detectors in some other corners so that you maximize the number of laser guns complemented with laser detectors, I suggest that you go read the full problem statement.
Now the first thing you may think about when solving this problem is that it’s composed of two parts, first part is knowing which corner B receives a laser beam from a laser gun put at corner A and this seems like a geometry problem, the second part is matching corners together to achieve the maximum number of laser guns complemented with detectors, this seemed like a maximum matching problem on general graphs, which is really tedious to implement.
First lets think about the underlaying graph structure, are those graphs really general ?
If we had a laser originated at A received at B, where will laser originated at B be received ?
Indeed a laser gun placed at B is received at A, after all it will have to travel through the same path but in reverse direction.
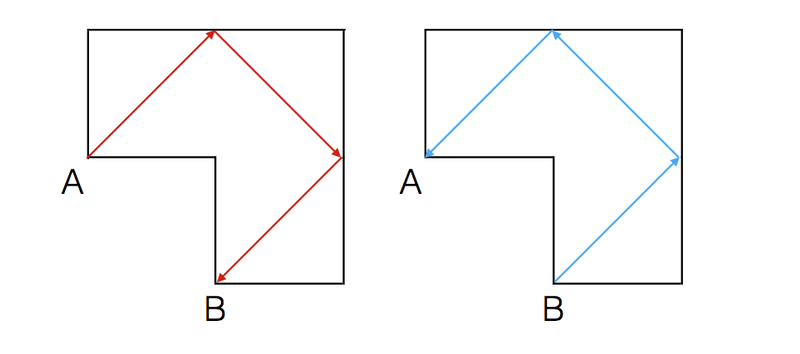
Can we have a laser originated at some corner and not end in some other corner ?
To answer this questions we first have to think about the set of points where a laser can hit, notice that :-
- All corner points have integer coordinates.
- Distance travelled between two successive hits in the X direction is equivalent to that travelled in Y direction , since the angle of the laser always 45, 135, 225 or 315.
It’s easy to show that if the point had integer coordinates then the next point will also have integer coordinates, since is either located on a vertical wall or a horizontal wall, lets assume it’s vertical (it’s X must be integer since the wall must have corners on both it’s ends) in this case we have integer thus the difference in Y is also integer, similarly we can show the same for horizontal walls.
thus the set of points where a laser can hit, is the set of all points with integer coordinates on the walls of the polygon, this set is finite and at most 300k as said in the problem’s constraints.
For a laser beam originated at a corner not to end on some other corner, then it has to wander infinitely jumping between those points on the walls and since they are finite then it has to cycle between them, Is this possible ?
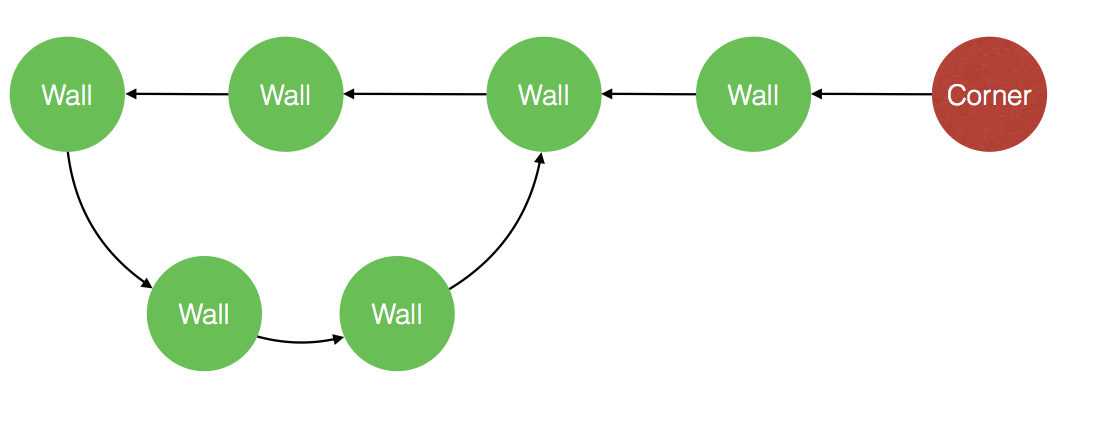
Of course this is impossible cause this means that we have a point receiving laser beam from two different sources into the same direction, then these two different sources have to be the same point.
This means that each laser beam must start and end in a corner, now we can conclude that the answer is always N/2, since each two corner points are paired with each other, they are also paired with some other wall points, so it’s like a graph having a number of connected components, each component has two corner points and some wall points.
Luckily simple rectilinear polygons always have even number of corners, so there’s no optimization problem here only the writer has tricked us to think there is, he also said if there’s more than one solution return any while the solution is always unique, Remember Don’t trust the writer.
Back to the geometry problem, how do we figure out which corners pair together ? How do we find the connected components of the graph ?
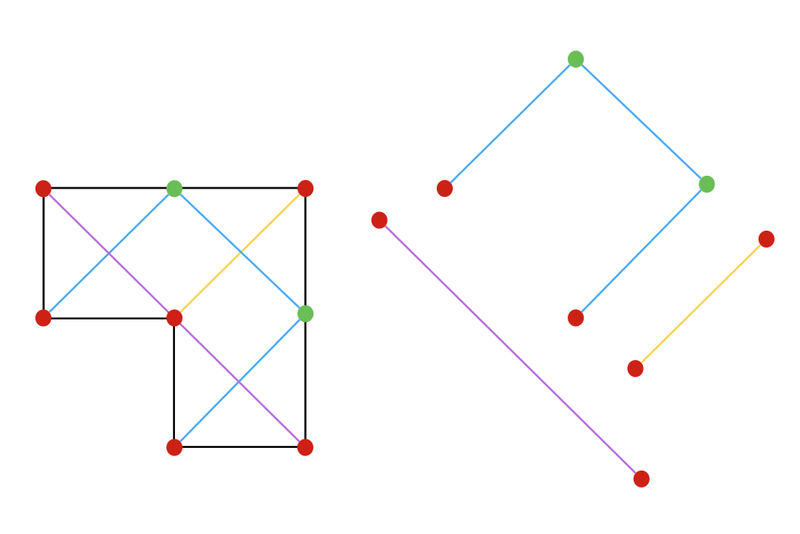
We only need to find the edges of the graph to find the connected components, i.e for each node find which node is next, which node is previous.
We can trace each laser beam, but the constraints are killer here this will never give us a full score.
But one might think would the problem be easier if those rays were vertical and horizontal ? instead of the 45 degreeish rays.
Only one way to find out, rotate the polygon by 45 degrees, However this will introduce floating point numbers, instead we rotate and scale by sqrt(2), making NewX = X - Y, NewY = X + Y.
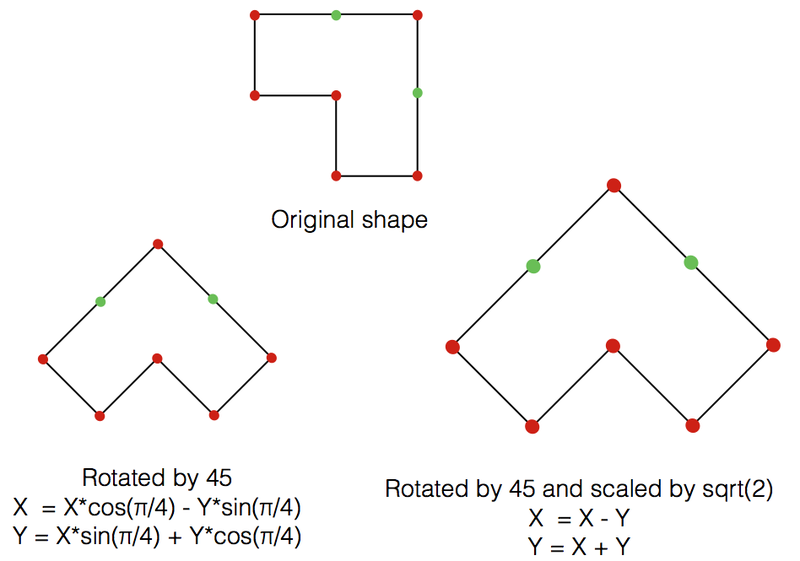
he points sorted by X value, then by Y value, an edge will often occurs between successive points having the same X value.
However there two cases we have to mind while doing the sweep
- Edges that occur outside the polygon should be ignored, this could be done by tracking whether we are inside the polygon or not (usually points alternate us between inside/outside/inside/outside.. the polygon so meeting a new point will often mean that we switch state)
- Handling cases where the ray touch a point but not reflected by this point.
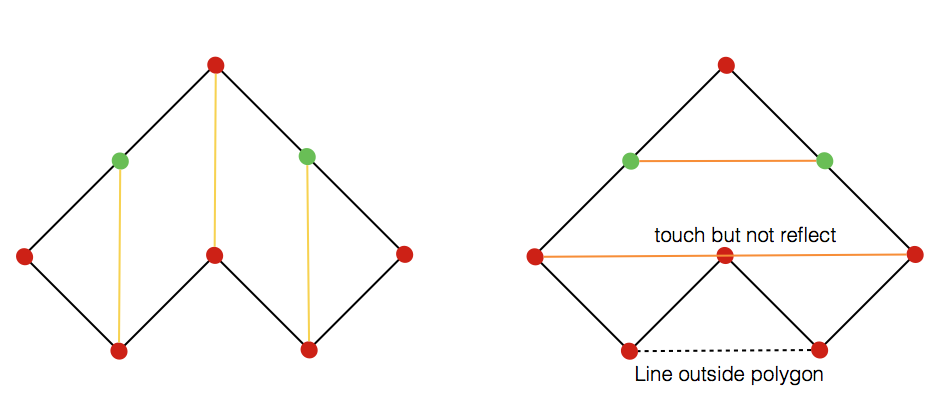
Similarly we can find horizontal edges, now that we have the edges of the graph we can find connected components and hence find the solution to the problem.
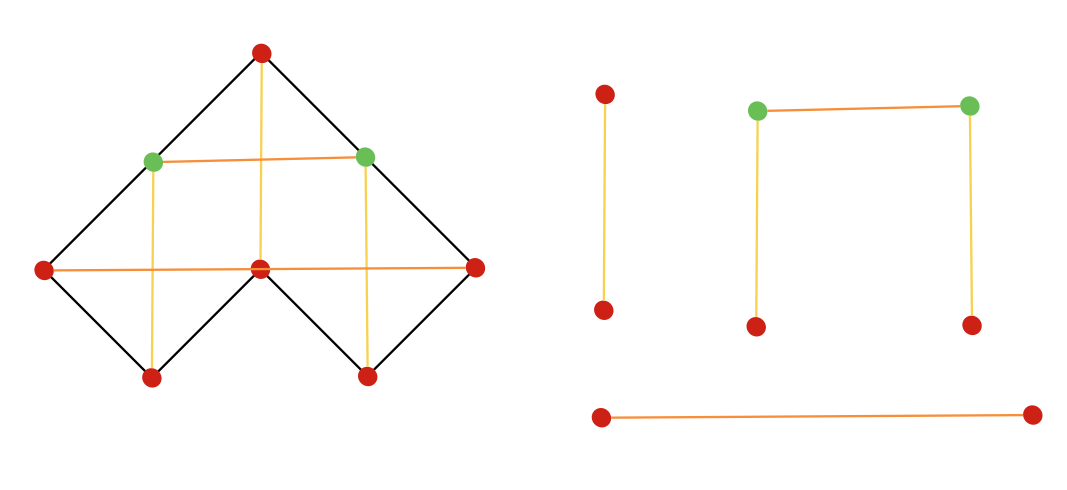
Now the question is How much would this problem change if we removed the integer point restriction and allowed real coordinates, does the start at a corner end at a corner condition still hold ? Feel free to comment with what you think.