Coprimes

Coprimes [ACM ICPC Regionals 2014 - Asia Anshan]

Given a sequence a of n integers ( $n ≤ 10^5$ ) where ( $a_i ≤ 10^5$ ), find the number of triplets (x, y, z) such that they are either pairwise coprime, or pairwise not coprime, feel free to check the problem statement for more explanation.

This problem was very interesting it combined various topics from combinatorics and number theory, first lets imagine each triplet as a triangle where the gcd of each pair of numbers is written on the side connecting them.

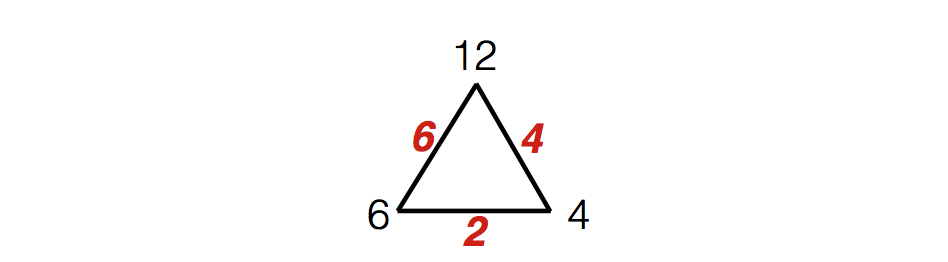
triangle

this seems like a lot of details, let’s just write 1 if the gcd is equal to 1, ≠1 otherwise, after doing this we would have four different types triangles.

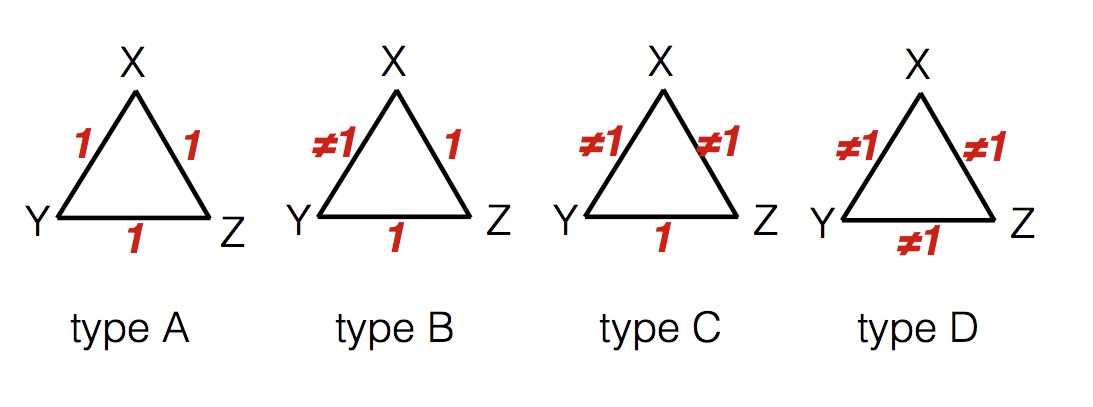
triangle_types

let’s call them type A, B, C and D, now the answer to the problem is count(A) + count(D), but how do we calculate that? We already know that $count(A) + count(B) + count(C) + count(D) = \binom n 3 = k_0$

So If only we could calculate count(B) + count(C) we could easily get the result by subtracting it from the previous equation.

Let’s fix some number as k can we calculate all triangles of type B and type C that has an left most vertex as k? call that f(k), we then have

$f(k) =\lvert x : x \in a \setminus k, gcd(x, k) ≠ 1\rvert * \lvert x : x \in a \setminus k, gcd(x, k) = 1\rvert$

Assume for now that we could calculate the cardinalities of those sets in a fast way, we’ll come back to this later, now if we sum f for all the numbers in the sequence what do we get ?

$\sum f(a_i) = 2 * count(B) + 2 * count(C) = k_1$

Not really what we expected, but why twice? we can have the same triangle while having a_i at X or at Y in case of type B, and at Y or at Z in case of type C.

However looking at what we got again

$count(A) + count(B) + count(C) + count(D) = k_0$ $2 * count(B) + 2 * count(C) = k_1$

This makes the answer to the problem $k_0 - k_1/2$ .

Now back to the part that we skipped which is how to calculate the cardinality of the sets we mentioned quickly.

We first have

$\lvert x : x \in a \setminus k, gcd(x, k) ≠ 1\rvert = n - 1 - \lvert x : x \in a \setminus k, gcd(x, k) = 1\rvert$

so it’s sufficient to calculate only one of them, let’s rewrite k as

$k = {p_0}^{a_0} * {p_1}^{a_1} * … * {p_r}^{a_r}$

to calculate $\lvert x : x \in a \setminus k, gcd(x, k) ≠ 1 \rvert$ , we need to calculate

$\lvert \{x : x \in a, p_0 \vert x\} \cup ... \cup \{x : x \in a, p_r \vert x\} \rvert$

For sake of simplicity let

$M_{p_i} = \{x : x \in a, p_i \vert x\}$

We calculate this using inclusion exclusion principle

$\lvert \cup_{0≤i≤r} M_{p_i}\rvert = \lvert M_{p_0}\rvert + \lvert M_{p_1}\rvert + … - \lvert M_{p_0 * p_1}\rvert - \lvert M_{p_1 * p_2}\rvert - … + \lvert M_{p_0 * p_1 * p_2}\rvert + …$

Notice here that we replaced the intersection by multiplication because a number that is divisible by both p and q has to be divisible by p*q, we find that each number which have an odd number of primes is added into the result, and each number that has an even number of primes is subtracted from the result, and we never used numbers which have a repeated prime.

This weight function we used is called Möbius function μ(n), and it has other applications, it’s defined as

μ(n) = 1 if n is square free and has odd number of prime divisors
μ(n) = -1 if n is square free and has even number of prime divisors
μ(n) = 0 if n is not square free

To implement this, we find that we have to iterate over the divisors of a number this is best done inversly, where each number goes to it’s multiples.

int freq[MAXN]; // freq[i]:count of times i occurs in the input 
int multiplesOf[MAXN]; // multiplesOf[i]:count of numbers divisible by i
int share[MAXN]; // share[i]:count of numbers sharing common div with i
int mu[MAXN]; // Möbius function
…
// initializing multiplesOf
for(int i = 2;i<MAXN;i++)
	for(int j = i;j<MAXN;j+=i)
		multiplesOf[i]+=freq[j];
…
// initializing share 
for(int i = 2;i<MAXN;i++)
	for(int j = i;j<MAXN;j+=i)
		share[j]+=multiplesOf[i] * mu[i];

After this precalculation we can calculate $\lvert x : x \in a \setminus k, gcd(x, k) ≠ 1\rvert$ in O(1) time and thus solve the problem.

Coprimes

Coprimes [ACM ICPC Regionals 2014 - Asia Anshan]

Additional resources