This strategy is usually applied when the search space is too large or infinite so it can’t be searched, it’s often used in geometry problems because usually the search space there is infinite, it can also be used to make your solution a lot simpler.
If the search space is large search space we try to find a subset of the search space satisfying the following condition:
If there’s a point in the whole search space which is a solution for the problem, then there is a point in the subset which is also a solution.
If the problem was an optimization (minimization) problem we can rephrase this as
If there’s a point in the whole search space that provides a solution with value v, then there is a point in the subset which provides a solution with value u≤v.
Say we wanted to find maximum independent set in a graph with N nodes, there’s subsets to try, however we can reduce the search space by knowing that a maximum independent set is also maximal, which means that we can’t add any more nodes to this set, so we don’t have to try all possible subsets we can only try maximal subsets.
For example lets say we have N intervals [Li, Ri] and we wanted to know if they intersect, there’s a smart way to do this but lets say we decided to iterate over all points of the search space [min(Li), max(Ri)] and check whether there’s a point that is inside all intervals or not!
All points in this space might be too much, or even infinite so lets look for that smaller subset that contains the solution
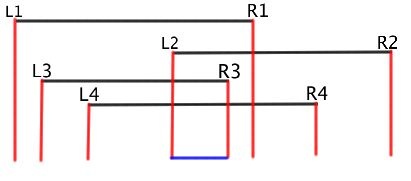
Looking at the example above we can see that the intersection of the intervals is [L2, R3], generally the intersection of a set of intervals is bounded by the start of some interval from the left and the end of some interval from the right.
Knowing this we can say that N intervals intersect if and only if the start of some interval Li lies in all the intervals, the same would work if we used Ri.
So instead of searching the whole space we can just consider all Li’s or All Ri’s which is a subset of this space.
Of course there’s a faster solution for this problem, but this is just an illustration.
Now we are ready to explore more problems
####TheTower [Topcoder SRM 423]
Lets start by first simplify the problem into the following problem, Given N checkers find the minimum number of moves to get them all in one cell. We need to find a point (u, v) such that is minimized.
We can rewrite this as which means that we can solve for x, and for y independently because the contribution to the result from x only depends on the value of u, and from y only depends on v.
Now the problem got even simpler we’re in 1D, so lets take a look at an example
Lets assume we have points on the x axis at 1, 3, 5, 6, 8 (colored in blue) Lets pick any point as u we picked 2 (colored in red)

Lets calculate sum of distances from red point to the blue points and call this value D D = 1 + 1 + 3 + 4 + 6
Now what happens if we move the red point one unit to the right? D = 2 + 0 + 2 + 3 + 5
D decreased by a value, this value is equal to (Number of points to the right of u - Number of points to the left of u)
This means that we can keep moving u to the right and obtain better result until we have number of points to the left of u equals number of points to the right of u, so for minimum D we should choose u as the median of the points, u = 5 in this example.
What if the number of points is even? any point between the middle two points would work, or even one of them (Try to prove it)
Now that we know that the best u belongs to x and best v belongs to y, we reduced the search space!
Back to the original problem where we don’t know the points that we want to minimize the distance to, but we know that those points are subset of the original points so the u for this subset belongs to the x’s of the original points and the v for this subset belongs to the y’s of the original points.
So it’s sufficient to try for each i all x’s, y’s of the original points and pick the tuple that minimizes the sum of the manhattan distances to it’s i+1 nearest neighbors.
Charging Chaos [Google Code Jam Round 1A 2014]
We know that the required buttons to switch must satisfy that each outlet after being switched will be equal to some device, and each device will have an outlet that is equal to it.
So instead of going through the $2^$) button switches, we choose one device (say the first device), and select some outlet for this device then we find the buttons we need to switch in order to make the outlet equal the device, if such a button switch satisfies the requirements for all other outlets and devices then it’s a candidate solution, thus we only need check N button switches and select the one that gives minimum number of switches.