So you know you’re solving an NP-hard problem, How can you put this into your advantage ?
Knowing the hardness of a problem can help a lot, for example if you know that the problem is hard, you shouldn’t waste time trying to find greedy algorithm that will never work.
Moreover if you’re solving a problem that looks a lot like a hard problem then it’s either really a hard problem, or there’s a little difference which would make this problem solvable.
Start by reading about some hard problems, those are some that I found useful in contests
Independent set, Vertex cover, Boolean satisfiability problem, Subset sum problem, Knapsack problem, Set cover problem, Exact Cover, Partition problem, Path cover, Hamiltonian path and Graph coloring.
It’s good to note that some of these problems become easy under specific constraints.
Here are some
- Checking if the graph has a 2 coloring (bipartite graph check), but not 3.
- Minimum vertex cover/Maximum independent set in a bipartite graph.
- 2-SAT, XOR-SAT.
Once you understand these problems, you can use them to prove that a problem is hard by doing reductions, you can read more about this in Introduction to Algorithms.
But what if the problem looked like a hard problem, but there was a little difference, this might be the key make it easier and get it solved.
Lets solve some problems that look like hard problems
Subset sum
Given an array A of numbers where each number is a power of two, determine if we can choose a subset of these numbers such that their sum is equal to a number X.
Having input numbers powers of two, should encourage us to take a look at the binary representation of X, more specifically the most significant bit.
If we have one number that has the same value as the most significant bit, we then should remove this number and subtract it from X and continue, otherwise we need to choose a subset of the numbers in A that sum to X remove them and subtract them from X and continue.
But which ones should we choose ? intuitively we should choose the larger numbers because smaller ones might be needed later for smaller bits.
for example if the numbers were {1, 1, 1, 1 2, 2} and we wanted to form 5, which is 101 in binary, if we choose {1, 1, 1, 1} to form the bit 100, we won’t be able to continue because we won’t have more 1’s, however if we choose {2, 2} we’ll be able to continue.
So the final algorithm would be, find the largest number in A ≤ X, if no such number exists then the answer is No, otherwise we remove that number from A and subtract it from X we repeat this while X > 0. The answer is Yes, if we end up with X = 0.
Exercise: prove that this algorithm is correct.
Infiltrate[ICPC WF 2012]
This problem looks a lot like a min set cover problem, or a dominating set problem.
Looking for differences or special properties we can see a line saying
For each pair of cells A and B, either A controls B or B controls A.
this means that the given graph is a Tournament, such a graph has some properties as
- Any subset of nodes also forms a tournament.
- In a tournament of size N, there exists a node that covers at least nodes.
From the above properties we can say that a greedy algorithm that keeps choosing the node that covers most uncovered nodes for a graph with 75 nodes we’ll need at most 6 nodes.
We can now use a brute force algorithm to find a cover of size 1, if none found then try 2, we should do this up to 5, if still none found we should use the greedy algorithm then.
Exercise: try to prove property 2, hint: number of edges in a tournament of size N is .
Seven kingdoms [ICPC Regionals NA-Rocky Mountain 2013]
The problem is asking us to partition the graph into 3 cliques, such that Winterfell (call this A) in one clique, King’s Landing (call this B) in another clique, and the rest of the graph is a clique.
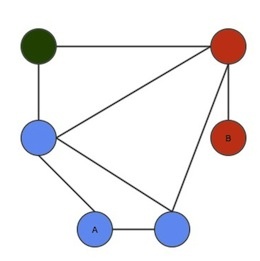
After drawing some random kingdom and solving, seeing cliques should give a little intuition that such a partition is hard, but that’s not enough to say that it’s hard.
One thing to try is to take a look at the complement of the graph.
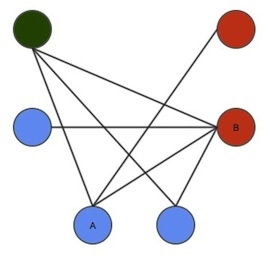
It seems like the problem here is asking for a 3-coloring for the complement of the graph which should make us sure that the problem is hard.
But there’s one line that says
There is no direct road between Winterfell (A) and King’s Landing (B) and they do not share a common neighbor city.
Lets call the first clique blue, second clique red, third clique green.
To construct a solution we observe that constraints come from the lack of edges, for example if the graph is complete we can easily find a solution, however these edges which does not exist in the graph imposes a constraint on us, that two nodes which are not connected by an edge cannot be colored with the same color.
Here are the constraints A is blue, B is red. If a node is not connected to A, and not connected to B then it must be green. If nodes X, Y are not connected by an edge then
- They can’t be both green, red or blue.
- If both of them are connected to A, then one of them is blue, the other is green.
- If both of them are connected to B, then one of them is red, the other is green.
What we have here is a series of implications for example if we chosen that X is green, then Y is for sure red or blue depending on whether Y is connected to A or to B.
This indicates that we can use 2-SAT to solve this problem, assume we have a boolean variable for each node in the graph call it G, where G_i is true if node i is green, we can use the above constraints to construct a boolean expression that is 2-CNF, If we solve this expression we can find the green nodes, other nodes can be determined to be blue or red depending on whether they are connected to A or B.
In the previous cases, most problems had something special that made it easier, however there are other problems which are hard, i.e there’s nothing special in the problem to make it easy, this is where you should think about a brute force solution, or exponential dynamic programming.
####Additional problems